calculating n-dimensional Graceli - integrals Graceli derived.

para variações e integração entre curvas de espirais.

{\ Int}

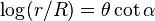\, \ Log (r / R) = \ theta \ Berço \ alpha

\pi

* Log θ / θ * pP [n] ,

{\ Int}

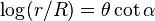\, \ Log (r / R) = \ theta \ Berço \ alpha

\pi

* Log θ / θ * pP [n],

{\ Int}

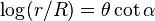\, \ Log (r / R) = \ theta \ Berço \ alpha

\pi

* Log θ / θ * pP [n] [n....]

Para Variações na Própria espiral.

{\ Int}

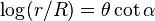\, \ Log (r / R) = \ theta \ Berço \ alpha

* Log θ / θ * pP [n] * log / lal / lal [n ...] * a * pp * Φ *

\ Lambda

.

Paragrafo θ Transversais Formando UMA tridimensionalidade dos Caracóis. e também Pará Dimensões Sete.
θ = Lal.
θ = lal * a * pp * Φ *

\ Lambda

. * R
θ = log / lal / lal [n ...] * a * pp * Φ *

\ Lambda

.
θ = lal * a * pp * Φ *

\ Lambda

.
θ = lal * a * pp *  Φ *
θ = lal * a * pp *
θ = lal * a *
θ = lal *

r = Rotação.
pP = Progressão SOBRE Progressão.

lal = latitude, Altura, longitude.
Φ *

\ Lambda

= Fluxos e Ondas.
θ = ÂNGULO Entre hum Ponto de latitude x Paragrafo Outro Ponto de longitude y, OU vice-versa.

Pará coordenadas Polares.

\, R (\ theta) = R e ^ {\ theta Berço \ alpha}

* Log θ / θ [n]

função Graceli para uma geometria de fluxos oscilatórios variados.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

* [ logΦ / Φ + pP * [a, R,0] ]* r.

pP = progressão com expoente de progressão.

[a, R,0] = alternância entre números reais e zero], ou seja, o zero representa um intervalo que desaparece.

geometria Graceli oscilatória.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

[ / , *, -, +]

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

* Φ * r.

Φ = fluxos.
r = rotação.

para a construção de tubos.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

para a construção de cones.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

* d * y

d = diâmetro.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

* log d / d [n]

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

[1] ,

{\int}

f'(x),\quad f''(x),\quad f'''(x)

\pi

[n...]

Geometria Graceli oscilatória integral.

para a construção de uma fita entre duas derivadas.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

[1],

f'(x),\quad f''(x),\quad f'''(x)

[2]

para a construção de um triângulo.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

[1] ,

f'(x),\quad f''(x),\quad f'''(x)

f'(x),\quad f''(x),\quad f'''(x)

[3].

para a construção de um quadrado ou outras formas geométricas.

{\int}

f'(x),\quad f''(x),\quad f'''(x)

[1],

f'(x),\quad f''(x),\quad f'''(x)

[2] ,

f'(x),\quad f''(x),\quad f'''(x)

[3],

f'(x),\quad f''(x),\quad f'''(x)

[4, n...].

quarta-feira, 13 de agosto de 2014